Secret Codes

Throughout history, people needed to hide messages:

Military commanders:

• Battle plans
• Troop movements
• Secret strategies

Spies and diplomats:

• Intelligence reports
• Treaty negotiations
• Secret alliances

Lovers:

• Private letters
• Secret meetings

The challenge: How do you send a message that only your friend can read, even if your enemies intercept it?

The solution: CIPHERS - secret codes that scramble your message!

Julius Caesar used this cipher to send military messages to his generals.

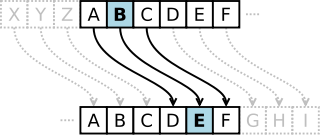
How it works: Shift each letter forward by a fixed number (usually 3).

Example: Shift by 3

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

Encrypting “HELLO”:

• H → K
• E → H
• L → O
• L → O
• O → R

Result: KHOOR

The weakness: Only 25 possible shifts! Try them all in minutes.

Ancient Hebrew cipher - the oldest known substitution cipher!

How it works: Reverse the alphabet: A↔Z, B↔Y, C↔X, etc.

Encrypting “HELLO”:

• H → S
• E → V
• L → O
• L → O
• O → L

Result: SVOOL

Fun fact: Encrypting twice gives you back the original!

• HELLO → SVOOL → HELLO

Arbitrary letter substitution - each letter maps to any other letter.

Encrypting “HELLO”:

• H → I
• E → T
• L → S
• L → S
• O → G

Result: ITLLG

But there’s a weakness! (We’ll discover it on the next slide)

The weakness: English letters appear with predictable frequencies!

Most common letters in English:

1. E (12.7%) - The champion!
2. T (9.1%)
3. A (8.2%)
4. O (7.5%)
5. I (7.0%)
6. N (6.7%)

How to break a substitution cipher:

1. Count how often each cipher letter appears
2. Most common cipher letter is probably E
3. Look for common patterns:
   • TH (most common digraph)
   • THE (most common word)
   • -ING (common ending)

Result: Even with 26! possible keys, you can break it in minutes!

Spartan military cipher - doesn’t substitute letters, it rearranges them!

How it works:

1. Wrap a strip of parchment around a wooden rod (scytale)
2. Write your message DOWN the columns (vertically along the rod)
3. Unwrap the strip → letters are scrambled!
4. Receiver wraps on same-diameter rod, reads down to decrypt

Example with 4-column rod:

Message: ATTACKATDAWNSENDHELP

Wrap parchment and write DOWN each column:
A K W D
T A N H
T T S E
A D E L
C A N P

Unwrap strip and read left-to-right:
Encrypted: AKWDTANHTTSEADELCANP

Receiver wraps on matching 4-column rod:
A K W D
T A N H
T T S E
A D E L
C A N P

Reads DOWN columns: ATTACKATDAWNSENDHELP ✓

The key: The diameter of the rod (number of columns)!

Weakness: Only rearranges letters, doesn’t hide their frequencies

Another transposition cipher - write in a zigzag pattern!

How it works (3 rails):

Write message in zigzag:

W . . . E . . . C . . . R . . . L . . . T . . . E
. E . R . D . S . O . E . E . F . E . A . O . C .
. . A . . . I . . . V . . . D . . . E . . . N . .

Original message: WE ARE DISCOVERED FLEE AT ONCE

Read off each rail:

• Rail 1: WECRLTE
• Rail 2: ERDSOEEFEAOC
• Rail 3: AIVDEN

Encrypted: WECRLTEERDSOEEFEAOCAIVDEN

To decrypt: Write in zigzag pattern again!

Leon Battista Alberti invented the first polyalphabetic cipher!

What’s polyalphabetic?

• Monoalphabetic: One substitution alphabet (Caesar, Atbash)
• Polyalphabetic: Multiple alphabets (changes during encryption!)

How it works:

• Two concentric disks with alphabets
• Outer disk (plaintext) fixed
• Inner disk (cipher) rotates
• Rotate the disk every few letters!

Why it’s revolutionary:

• Same letter encrypts to different letters each time!
• ‘A’ might be ‘D’ first time, ‘M’ second time
• Defeats frequency analysis!

This idea led to the Vigenère cipher…

Blaise de Vigenère created a cipher that resisted breaking for 300 years!

How it works: Use a keyword to determine shifts (like multiple Caesar ciphers)

Example - Keyword: “PASS”

P = 15, A = 0, S = 18, S = 18 (A=0, B=1, C=2, ...)

Plaintext:  A T T A C K A T D A W N
Keyword:    P A S S P A S S P A S S
Shift by:   15 0 18 18 15 0 18 18 15 0 18 18
Ciphertext: P T L S R K S L S A O F

Why it’s strong:

• ‘A’ encrypts to P, then R, then S (different each time!)
• Different keyword → completely different cipher
• Defeated frequency analysis for 300 years!

The weakness: The keyword repeats…

Decrypt this message with keyword “DOG”:

KSYWWG

Remember: D = 3, O = 14, G = 6

Hint: Use the Vigenère square to help!

The perfect cipher - proven mathematically unbreakable by Claude Shannon (1945)!

How it works:

1. Create a truly random key, same length as message
2. Use each key letter exactly once (never reuse!)
3. Add key to plaintext (mod 26)

Example:

Message: HELLO
Key:     XMCKL (truly random, never reused)
Cipher:  EQNVZ

H(7) + X(23) = 30 mod 26 = 4 = E
E(4) + M(12) = 16 = Q
L(11) + C(2) = 13 = N
L(11) + K(10) = 21 = V
O(14) + L(11) = 25 = Z

Why it’s unbreakable:

• Every possible message is equally likely!
• No pattern to analyze
• Information-theoretically secure

Why it’s rarely used:

• Key must be truly random (hard!)
• Key must be as long as message (impractical!)
• Key must never be reused (dangerous if violated!)
• Key distribution problem (how to share securely?)

Claude Shannon (1916-2001)

Not a cipher - replace entire words or phrases with code numbers!

Example codebook:

ATTACK          → 4729
RETREAT         → 8331
REINFORCEMENTS  → 2156
AT DAWN         → 7743
SEND            → 3891

Message: “SEND REINFORCEMENTS AT DAWN”

Encoded: 3891 2156 7743

Advantages:

• Very secure if codebook is secret
• Can’t use frequency analysis on words
• Compact (numbers shorter than words)

Disadvantages:

• Codebook can be captured!
• Limited vocabulary
• Everyone needs same codebook
• Can’t express new concepts not in book

Famous example: Zimmermann Telegram (WWI) - helped bring USA into war!

The code that changed World War I!

January 1917: German Foreign Minister Arthur Zimmermann sent an encrypted telegram to Mexico:

The secret proposal:

• Germany would help Mexico reconquer Texas, New Mexico, and Arizona
• In exchange, Mexico would ally with Germany against the USA
• Promise: “Generous financial support”

The British intercept and decrypt it!

The Room 40 codebreakers (Britain’s secret cryptanalysis team) had partially broken the German diplomatic code.

March 1917: Britain shares the decrypted telegram with the USA

American public is outraged!

April 6, 1917: USA declares war on Germany

Result: The telegram helped bring the USA into WWI, tipping the balance toward Allied victory.

Combination of substitution + transposition - two-stage encryption!

Why “ADFGVX”? These letters are very different in Morse code (less errors in transmission)

Step 1: Fractionating Substitution Use 6×6 grid (includes digits):

    A D F G V X
  ┌─────────────
A │ 8 p 3 d 1 n
D │ l t 4 o a h
F │ 7 k b c 5 z
G │ j u 6 w g m
V │ x s v i r 2
X │ 9 e y 0 f q

Each letter becomes a pair:

• “ATTACK” → AT,TA,CK:
• A(row D, col G) → DG
• T(row D, col D) → DD
• T → DD
• A → DG
• C(row F, col G) → FG
• K(row F, col D) → FD

Result: DG DD DD DG FG FD

Step 2: Columnar Transposition (scramble the pairs with keyword)

Very strong for its time! Resisted Allied cryptanalysis for months.

French cryptanalyst Georges Painvin broke ADFGVX in one of the greatest feats of cryptanalysis in history!

The challenge:

• Two-stage encryption (substitution + transposition)
• Germans changed keys frequently
• Painvin had to work from intercepted ciphertext only

His breakthrough:

• Noticed patterns in the fractionated pairs
• Used statistical analysis
• Worked backwards through both stages
• Took months of exhausting work

June 1918: Painvin broke the cipher during the German Spring Offensive

The intelligence revealed:

• German attack plans
• Troop movements
• Strategic positions

Result: Helped French forces repel the offensive, contributing to Allied victory

The cost: Painvin lost 33 pounds and had a nervous breakdown from the intense mental effort!

Georges Painvin (1914)

The next evolution: Mechanical cipher machines with rotating wheels!

How rotors work:

• Each rotor is a substitution cipher (26 wires connecting letters)
• Rotors rotate with each keystroke
• Multiple rotors create polyalphabetic cipher
• Millions of possible combinations!

Early rotor machines:

Hebern Rotor Machine (1917, USA)

• First electric rotor machine
• Single rotor (not very secure)

Kryha Machine (1920s, Germany)

• Mechanical rotors
• Used by diplomatic services
• Broken by cryptanalysts

These ideas led to the most famous cipher machine in history…

Coming next: The Enigma Machine!

By the 1920s, codebreakers had learned to crack every cipher through:

• Frequency analysis
• Pattern recognition
• Statistical methods
• Cribs (guessed plaintext)

The Germans thought: “What if we made a cipher so complex that even WITH these techniques, it would take years to break?”

Enter: The Enigma Machine (1923)

• Multiple rotors
• Plugboard scrambling
• Reflector (making encrypt = decrypt)
• ~10²³ possible settings per day

The challenge: Could anyone break a cipher with quintillions of possible keys?

The hero: A young British mathematician named Alan Turing…

Next lesson: How Turing and his team broke the “unbreakable” Enigma!